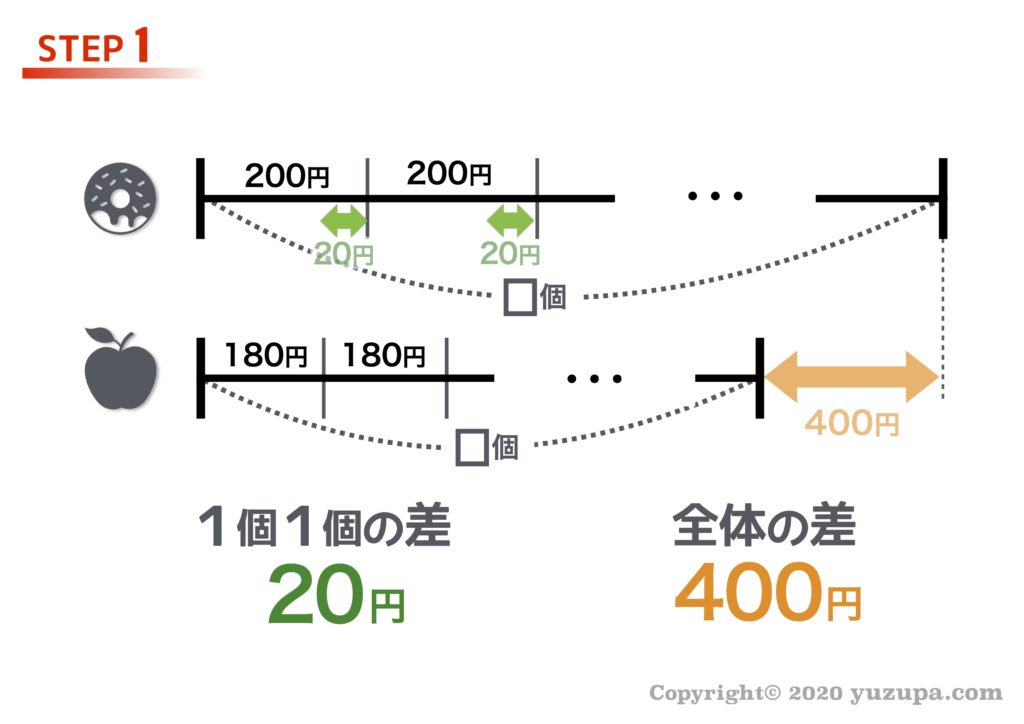
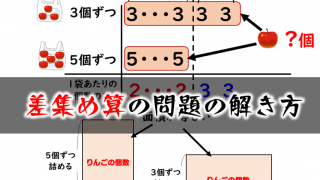
過不足 (かふそく)は、多すぎることと足りないことを意味し、 余ったり不足したりすることから全体の差を求め、それを1人分の差で、 割ることによって人数を求める、差集め算の一つです。 方法としては、面積図を用いる方法、線分図を用いる方法が 差集め算は、「1個あたりの差」と「全体の差」から個数を 求める問題です。 全体の差÷1個当たりの差=個数 こんな問題です。 「何個かのケーキを4個ずつ箱につめると、6個ずつ箱に つめるときと比べて3箱多くなる。 ケーキは何個ありますか 中学受験に塾なしで挑戦するブログ―やってみ つるかめ算の解き方のテクニック・応用編 線分図に表すと、長さは 1 × となり、これは 翼くんが持っていたお金 となります。 (実際) 105円の青鉛筆を 本買い、更に105円の青鉛筆を2本買い、90円余った この2本の線の長さは、最初に 翼くんが持っていたお金 と同額です。 また、赤・青鉛筆をそれそれ 本を買った時の差額は 105 × 2 90 = 300 円 ① となります

中学受験算数 これだけ 算数のカギ 文章題 差集め算 1つあたりの差 Spi Youtube
差集め算 教え方
差集め算 教え方-算数の教え方講座 差集め算・過不足算(応用) https//10kensite/osiekata/ 算数の教え方講座 差集め算・過不足算(応用) https//10kensite こんにちは!麻布先輩です。 今回の中学受験算数入試問題は洛南高校附属中から「差集め算」に関する問題です。 和や差に関する問題の中でも「差集め算」は昔からよく入試問題に出題されますよ。 今回のように金額の違う商品を買うパターンは特に多いです。




4年生向け 中学受験 算数 差集め算入門 その2 差集め算の基本について例題とともに解説します Youtube
単元の解説・教え方 「差集め算」とは、単位量あたりの個数の差から全体の量を求める問題です。 「過不足算」は差集め算と似ていますが、単位量あたりの個数の差と過不足をヒントに全体の量を求める問題です。 「 和差算」とは、2つの数値の和や差からそれぞれの値を求める問題です。 「 つるかめ算」とは、複数の種類のものがあってその総数が与えられた 3個ずつ配る場合と、5個ずつ配る場合では、 1人がもらえる数の差 は 5 – 3 = 2 個 となります。 線分図より、 人に3個ずつ、5個ずつ配った時の差は、 6 10 = 16 個 となり、これは、1人がもらえる数の差 5 – 3 = 2 個の集合体 となります。 よって、 16個の差ができる人数 は、 16 ÷ 2 = 8 人 よって、一箱に入っていたみかんの数は、 (3個配ったことから計算する 旅人算の基本は、2人の距離の差や和、速さの差や和を考えます。問題文を読んで、追いつくのか、出会うのかを考えるようにしましょう。それでは、具体的に4つのパターンを具体的な例を上げながら、考え方と解き方を紹介します。 11 同じ道で追いつく これは、先に誰かが出発して、も
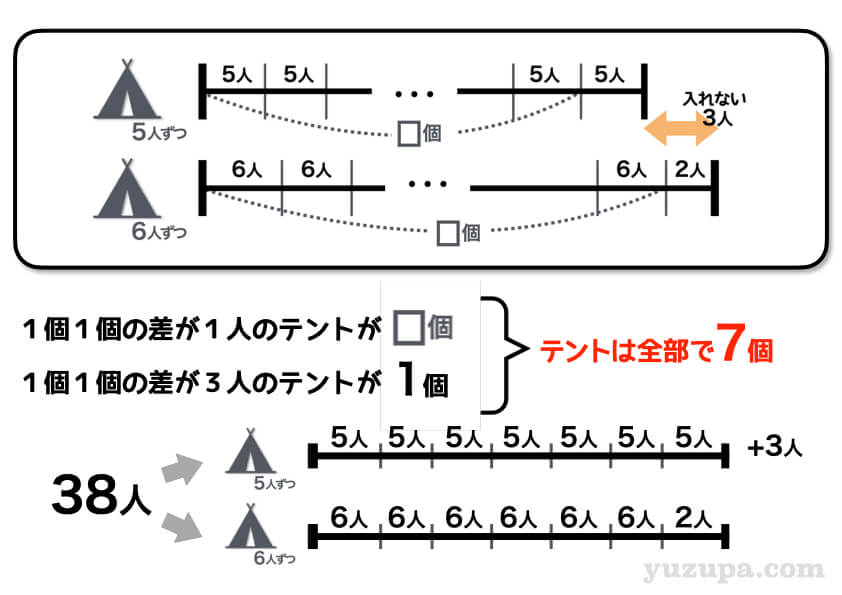
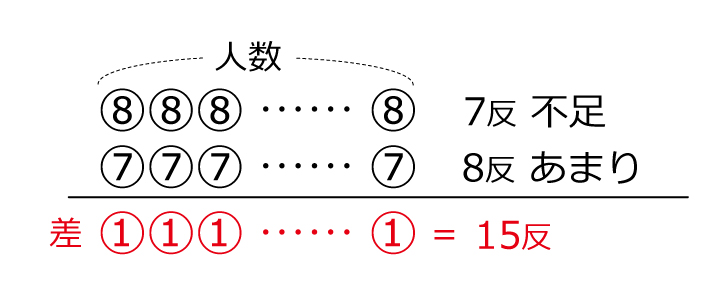
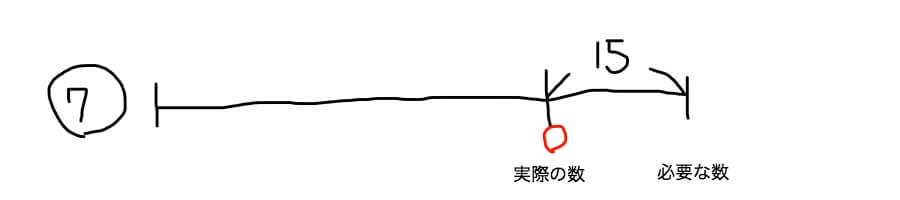
盗人算(過不足算・差集め算) 盗人算(ぬすびとざん) 中学受験の算数では,過不足算や差集め算と呼ばれる問題です。テキストの例題レベルの問題です。 盗人が橋の下で絹を分け合います。8反ずつ分ければ7反が足りません。また,7反ずつ分ければ8反があまります。盗人は何人いますか差集め算→基本問題(浅野中学 10年) 生徒の宿泊で、1室の定員を5人ずつにすると全部の部屋を使っても4人分足りなくなり、1室の定員を6人ずつにすると5人の部屋が1室でき、1室が余ります。 このときの生徒の人数を求めなさい。 考え方と答え スマートホンアプリつるかめ算の考え方の極意は、 この「全部〇〇だったら?」と仮定する ところに尽きます。仮定してから、実際の数値との差を考えていくのです。これは面積図を使っても使わなくても重要な考え方のひとつです。 まずは、「全部かめだったら?」というところから考えてみましょう。 上の
到着時刻が前後する例題(速さ差集め)の解き方 3分前に着くなら、始業時刻には学校を通り過ぎてる、っておもしろいね。 はるか Haru_You 始業時刻まで歩いたときの位置でそろえたいからね。 速さの差集め算は、指定時刻まで進んだときの道のりの差÷速さの差=指定時刻までの時間Hello School 算数 差集め算 練習問題 解答と解説 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。 1. りんごとみかんが同じ個数あります。何人かにりんごを6個ずつ、みかんを3個ずつ 配ったら、りんごは2個、みかんは17個余りました。りんごとみかんは何個ずつあり差集め算 基礎編 今回は、差集め算です。 次の問題を解いてみましょう。 制限時間は2分です。 『あるクラスの人にアメを一人ずつに3個配ると16個余り、一人ずつに5個配ると4個余る。 アメは全部で何個ありますか? 』 解法1 2つの状況を比較する




中学受験 差集め算とは 基本問題はできるのに応用問題ができない理由 かるび勉強部屋



中学受験 差集め算とは 基本問題はできるのに応用問題ができない理由 かるび勉強部屋
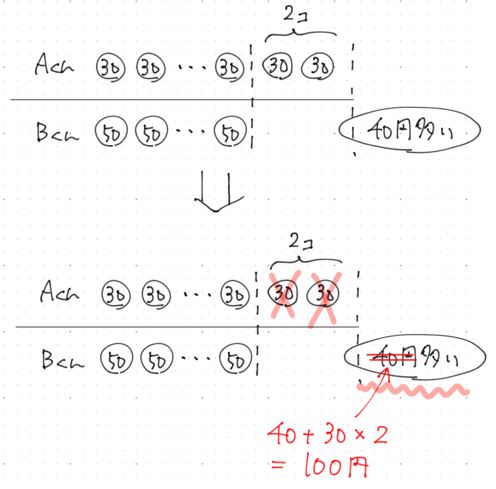
アップ攻略法① 差集め算 → 同じ個数に合わせて線分図を描け! (1) 「差集め算」ときたら → 「同じ個数にそろえて、線分図を描け!」 を絶えず意識させろ! (2) 「1個の差」を → 「同じ個数集めて」 → 「全体の差」とする!を徹底的にマスターさせろ!差集め算⑴ 基本 1 ステップ1 同じ個数の問題① 代金の差 1 A君は1個100円のお菓子 かし を、B君は1個70円のお菓子を同じ数ず つ買ったところ、2人がはらった金額の差は210円でした。このと き、( )にあてはまる数を求めなさい。 ⑴ 2人が買ったお菓子の1個あたりの値段の差は、 ( )−過不足算 過不足算とは 過不足算とは、ある個数の物を2種類の方法で配った時に、 個余ったり、 個足りなくなったりする問題です。 線分図を書いて解く人と、面積図を書いて解く人がいますが、ここでは面積図を使った解き方を解説していきます。 面積




中学受験算数 差集め算 小学4年生 6年生対象 毎日配信 Youtube




4年生向け 中学受験 算数 差集め算入門 その2 差集め算の基本について例題とともに解説します Youtube
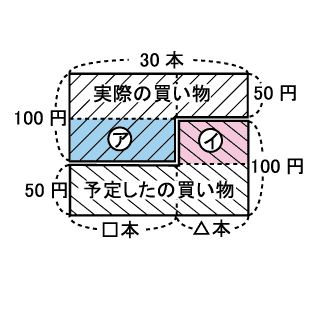
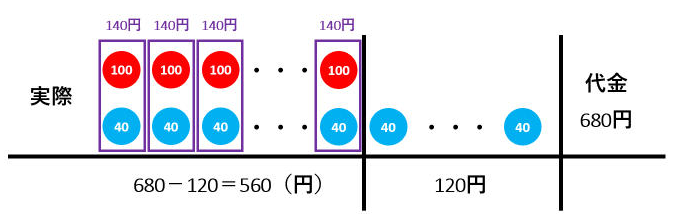
ニュートン算の徹底演習50問 中学受験算数の「ニュートン算」を完璧にするために、50問の演習プリントを作成しました。3レベルに分けてありますが、レベルaが必修問題、レベルbがr4や 通過算の徹底演習50問とりちがえの問題(差集め算)と解き方 Posted on by hpa in 単元別の研究, 和と差の問題 // 0 Comments とりちがえの問題1 00円もって,みかん12個とりんご8個買って,おつりを80円もらうはずだったのを,まちがえてみかんとりんごの個数を取り違えてしまたの 「差集め算 」は線分図の 作成中中学受験食塩水(濃度)の図・公式・問題の解き方など総まとめ 中学受験植木算の教え方の2つのコツ!小学3年生にも分かりやすい プリント31枚!植木算とは?基礎から応用まで全部まとめま




全体の差 と 1つあたりの差 に注目しよう 過不足算 差集め算の解き方 中学受験ナビ




差集め算 の2つの解き方を解説 中学受験に出る文章問題 数学fun
7差集め算 テーマ: 受験算数 面積図 今回は、 「長方形を重ねて考える」 という面積図の使い方をやりたいと思います。 まずは基本的な考え方を説明します。 これを利用して、実際に問題を解いてみます。 青い長方形と赤い長方形が第3回 分配算・差分け算 斎藤講師(鉄人会スーパープロ家庭教師) 今回は決められた割合にしたがってお金などを分配する問題を考えます。その中で,もとにする量(基準量)が同じ問題だけを取り上げますが、これはもとにする量(基準量)が異なる問題への基礎となるとらえ方ですから旅人算の問題:A町を太郎君が,B町を次郎君が同時に出発し, 両町の間をそれぞれ1往復しました。このとき,2人が最初に出会ってから・・・また 2人が最初に出会ったのはB町から48kmの地点で, 2回目に出会ったのはA町から・・・地点でした。これについて,次の問に答えなさい。



中学受験 差集め算の解き方は3パターン 線分図を書きましょう




中学受験算数 これだけ 算数のカギ 文章題 差集め算 1つあたりの差 Spi Youtube
インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。 1. りんごとみかんが同じ個数あります。 何人かにりんごを6個ずつ、みかんを3個ずつ 配ったら、りんごは2個、みかんは17個余りました。 りんごとみかんは何個ずつあり ましたか。 2. 1個80円のアンパンを何個か買う予定のお金を持って店に行きました。これが和差算の考え方です。 多い方から差の分を取り除き、それぞれを同じ数にする。 そのときの合計から、小さい方の数を求めることができる。 この考え方を思いつくのは難しいですが、知ってしまえば利用することは簡単です(^^) それでは、サクッと練習問題に挑戦してみましょう。 練習 差集め算は面積図(ア=イ)・図表(公式!)で解く!(文章題)―「中学受験+塾なし」の勉強法・教え方 でした。 全体の差÷1個当たりの差=個数 です。これを面積図や図表で整理していくのが基本です。



中学受験 差集め算の解き方は3パターン 線分図を書きましょう




差集め算 の2つの解き方を解説 中学受験に出る文章問題 数学fun
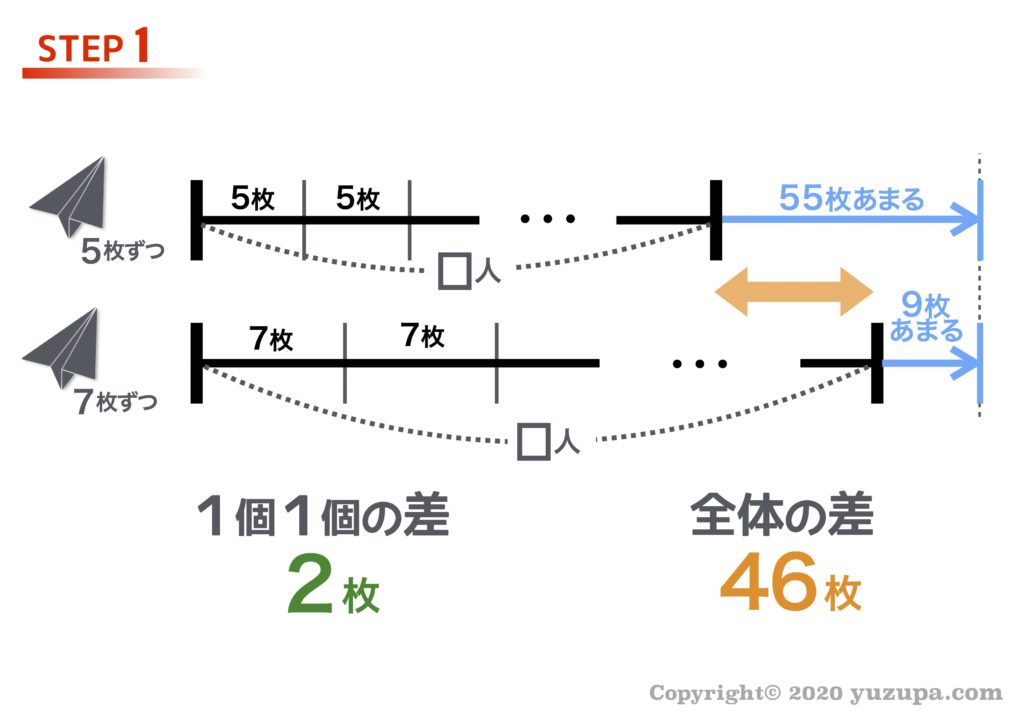
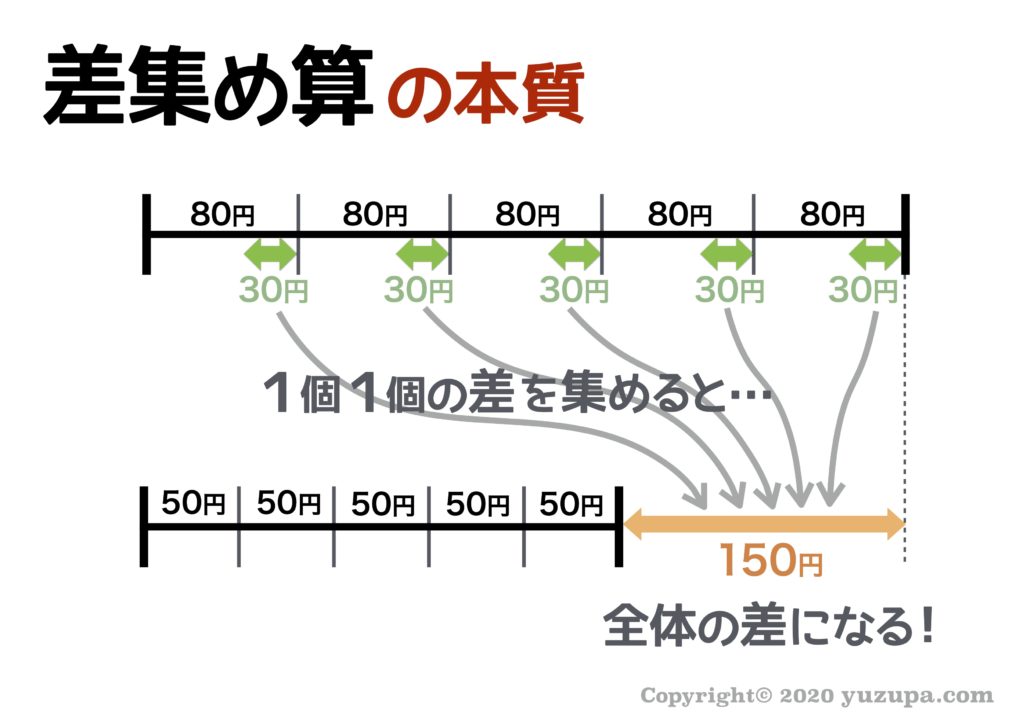
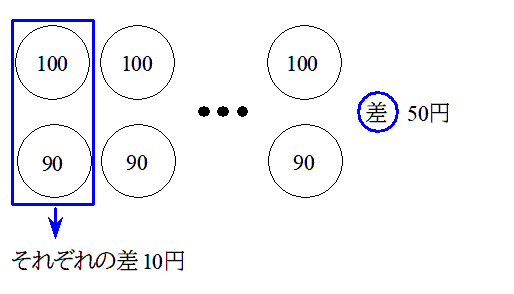
過不足算の教え方 つるかめ算に続いての教え方シリーズです。 まず、過不足算の紹介です。 差集め算と呼ばれることもあり、参考書では過不足算・差集め算と併記されることもあります。 つるかめ算と同じ「和と差に関する問題」のグループに所属していて、そのグループの中では難度の高い単元です。 「和と差に関する問題」は、特殊算と呼ばれる つまり、〔1袋あたりの差〕が〔袋の数〕だけ集まって〔全体の差〕になるのだから、 〔1袋あたりの差〕×〔袋の数〕=〔全体の差〕 〔全体の差〕÷〔1袋あたりの差〕=〔袋の数〕 となります。 これが、差集め算の基本の考え方です。 では、例題を考えてみましょう。 ここで大切なことは、袋の数を同じにそろえて差を考えるということです。 12個ずつ "差集め算" とはナニモノか? "差集め算" とは? 差集め算とは "1個1個の差" を全て集めると "全体の差" になる という真理を使う問題。これだけ読んでもちょっと話分かりづらいかと思いますので 80円切手と50円切手の具体例をみてみましょうd(^_^o)




差 集め 算 面積 図 ニスヌーピー 壁紙



中学受験 差集め算とは 基本問題はできるのに応用問題ができない理由 かるび勉強部屋
先日は、第9回の差集め算を教えました。 私は、5年生の算数ならば予習は行っていません。 多くの講師がそうだと思います。 逆に言えば、それができない講師は、教えられるかもしれませんが、設計図を描けないといいますか、長期的な展望による体系立てた指導はできないと思います。 ①差集め算 配っていったときにどちらかがきっちり配れるタイプの問題です。 人数(個数)=全体の差÷1つあたりの差(配り方の差) で解けます。慣れるまでは線分図を書いてみましょう。 ②過不足算 どちらもきっちり配れないタイプの問題です。 ★ 単元の話なので、興味の無い方はまったく面白くはないと思います。 過不足算は、サピックスでは4年生で学習し、四谷大塚では5年生前期に学習し、日能研では5年生後期に学習します。 サピックスと日能研では過不足算と呼んでいますが、四谷大塚では差集め算と呼んでいます。 意味を



Math 過不足算 差集め算の応用問題 働きアリ




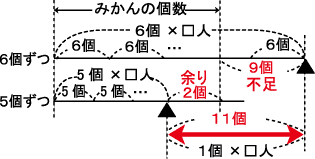
中学受験 差集め算 まちがえて配ったアメの数から子供の人数を求めるには さんすうがく
差集め算の公式で覚えておくのはひとつ ひとつの差を集めると全体の差になる ということです。 公式 ひとつの差 × 個数 = 全体の差差集め算とは 「差集め算」とは、単位量あたりの個数の差から全体の量を求める問題です。 実際に例を見たほうが分かりやすいでしょう。 差集め算の例題1 りんごがいくつかあり、これらを袋に3個ずつ詰めると、5個ずつ詰めたときと比べて2袋多くなる。 どちらの場合も過不足なくきっちりりんごが詰められる場合、りんごは全部で何個あるか求めよ。 このよう 1あたりの差の集まりを使って解く問題を差集め算、『〜すると 余る、〜すると 足りない』といった問題を過不足算といいます。 解き方は線分図や面積図で考えるのが一般的ですが、基本的な問題は式を作るだけで考えることが出来ま




中学受験 特殊算は何種類ある 算数の文章題の見分け方 かるび勉強部屋 中学受験 勉強 中学数学




動画解説 みんなの算数オンライン ここで差がつく超頻出の差集め算問題




差集め算 の2つの解き方を解説 中学受験に出る文章問題 数学fun



中学受験 差集め算とは 基本問題はできるのに応用問題ができない理由 かるび勉強部屋



差集め算の面積図利用法 中学受験ー算数解き方ポータル



差集め算の基本問題16題をひたすら解くページ 解き方もあり〼 チャンプルー



1




差集め算 の2つの解き方を解説 中学受験に出る文章問題 数学fun




差集算 差集め算 線分図と面積図で解こう



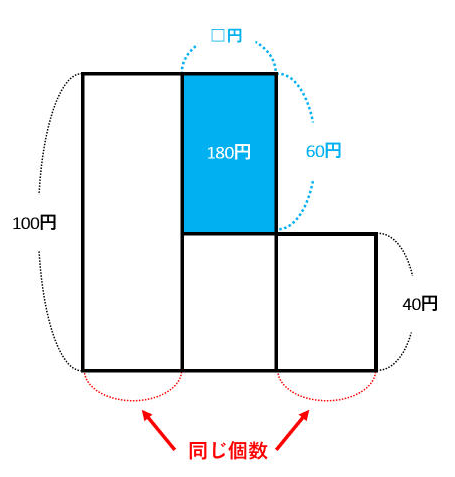
第2章 差集め算の 偏差値アップ 指導法 例題 中学受験の勉強法 偏差値アップの学習法




算数文章題講座 差集め 過不足算の解き方 基本問題



差集め算 とりちがえ問題を表 面積図 消去算で解いてみよう みみずく戦略室




つるかめ算 差集め算の考え方 整数範囲 中学受験基礎 サイパー思考力算数練習帳シリーズ M Access 本 通販 Amazon




算数文章題講座 差集め 過不足算の解き方 基本問題




7 差集め算 青空塾の教え方



差集め算 の文章問題 計算ドリル 問題集 数学fun



中学受験 差集め算とは 基本問題はできるのに応用問題ができない理由 かるび勉強部屋



1




算数文章題講座 差集め 過不足算の解き方 基本問題



中学受験算数 差集め算 再入門 中学受験プロ講師ブログ




偏差値20アップ指導法 より 差集め算 Youtube




7 差集め算 青空塾の教え方



差集め算が分からない 教え方のコツとは 文章問題編 オンライン家庭教師 スタディメンター



差集め算の基本問題16題をひたすら解くページ 解き方もあり〼 チャンプルー




中学受験 差集め算とは 基本問題はできるのに応用問題ができない理由 かるび勉強部屋
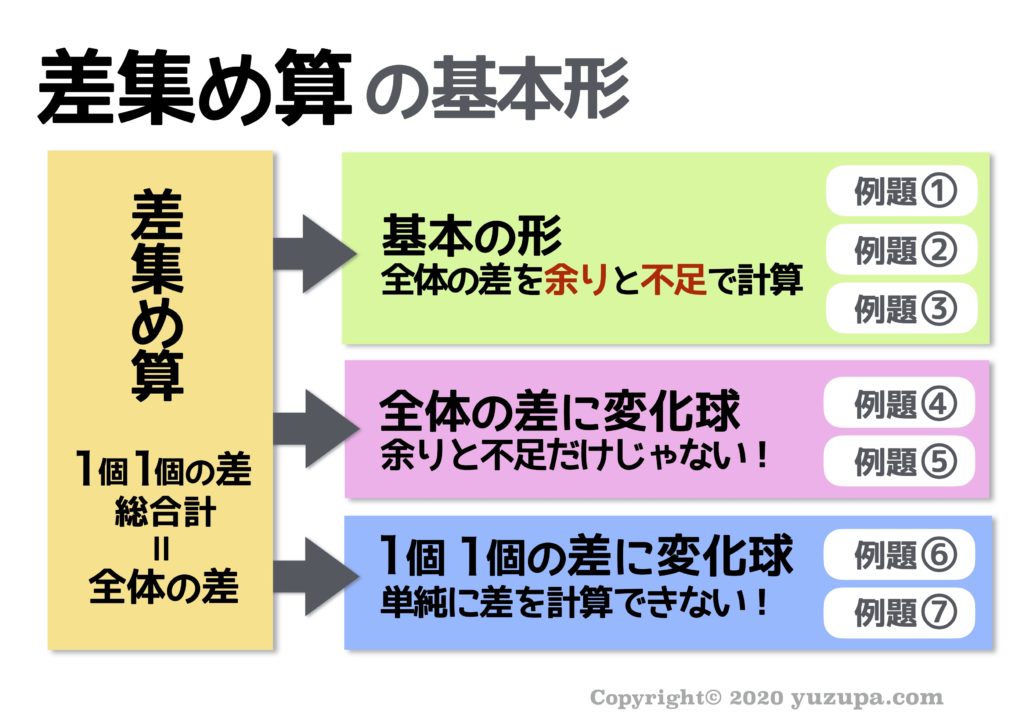



中学受験 差集め算とは 基本問題はできるのに応用問題ができない理由 かるび勉強部屋




差集め算その5 とりちがえの問題 Youtube




中学受験 差集め算とは 基本問題はできるのに応用問題ができない理由 かるび勉強部屋
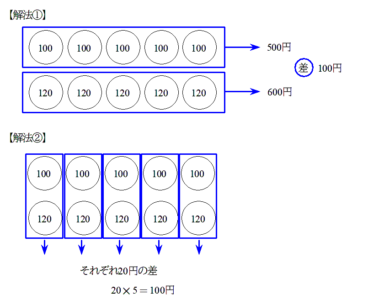



差集め算が分からない 教え方のコツとは 文章問題編 オンライン家庭教師 スタディメンター
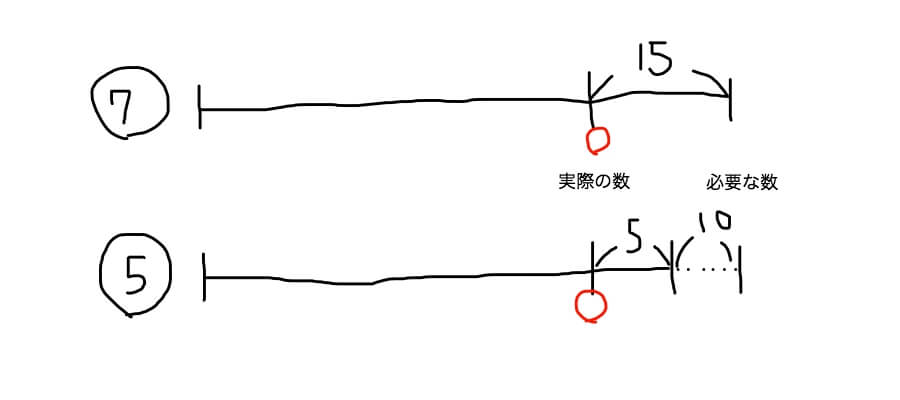



中学受験 差集め算の解き方は3パターン 線分図を書きましょう




過不足算 の3パターンの解き方を解説 中学受験に出る文章問題 数学fun




過不足算 差集め算 第1回 過不足算 差集め算の基本的な考え方 解き方 算数パラダイス




差集め算 過不足算 つるかめ算 消去算 古川俊 本 通販 Amazon
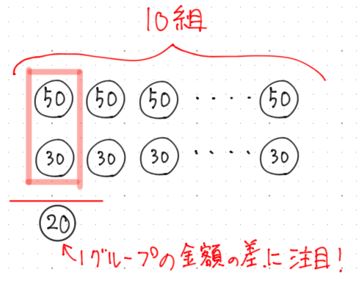



中学受験算数 差集め算 再入門 中学受験プロ講師ブログ




差集算 差集め算 線分図と面積図で解こう




差集め算 の2つの解き方を解説 中学受験に出る文章問題 数学fun



和算 第4回 盗人算 小学生でもわかる塵劫記 じんこうき 算数星人の中学受験お役立ち情報



中学受験 差集め算の解き方は3パターン 線分図を書きましょう




差集め算 の文章問題 計算ドリル 問題集 数学fun




算数の教え方講座 差集め算 過不足算 基本 10ken Site Osiekata Youtube




差集め算 の2つの解き方を解説 中学受験に出る文章問題 数学fun
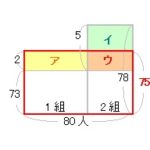



差集め算は面積図 ア イ 図表 公式 で解く 文章題 中学受験 塾なし の勉強法 教え方



第2章 差集め算の 偏差値アップ 指導法 例題 中学受験の勉強法 偏差値アップの学習法




中学受験 差集め算とは 基本問題はできるのに応用問題ができない理由 かるび勉強部屋
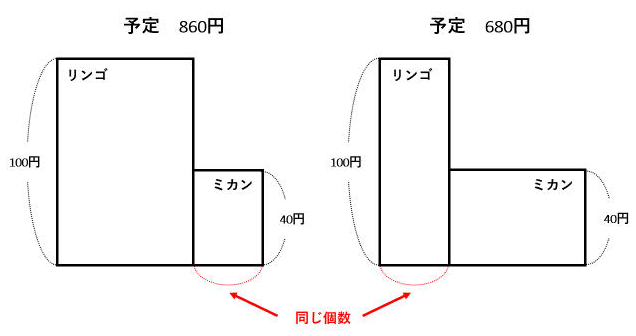



差集め算 とりちがえ問題を表 面積図 消去算で解いてみよう みみずく戦略室




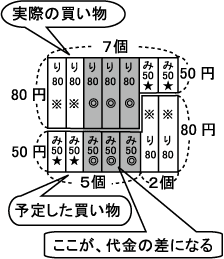
中学受験 差集め算 商品の個数と金額の差から 買った商品の個数を求めるには さんすうがく




中学受験 算数 12月 差集め算 旅人算 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




差集め算なんて教えなくても自力で解ける O 受験に強くなる子どもとの接し方




Newみんなの算数講座52 差を集めるという考え方 中学受験の算数知恵宝庫




差集め算 過不足算の基本問題 Youtube




差集め算は面積図 ア イ 図表 公式 で解く 文章題 中学受験 塾なし の勉強法 教え方




差集め算の解き方と問題一覧 中学受験の算数 理科ヘクトパスカル




過不足算 の文章問題 計算ドリル 問題集 数学fun




差集め算その5 とりちがえの問題 Youtube




四谷大塚の差集め算は難しすぎる 中学受験の算数を極める




差集め算 の2つの解き方を解説 中学受験に出る文章問題 数学fun




差集算 差集め算 線分図と面積図で解こう



過不足算 差集め算 基礎から入試問題まで 父ちゃんが教えたるっ




つるかめ算 差集め算の考え方 整数範囲 中学受験基礎 サイパー思考力算数練習帳シリーズ M Access 本 通販 Amazon




差集め算は面積図 ア イ 図表 公式 で解く 文章題 中学




差集め算 の2つの解き方を解説 中学受験に出る文章問題 数学fun




中学受験 差集め算とは 基本問題はできるのに応用問題ができない理由 かるび勉強部屋
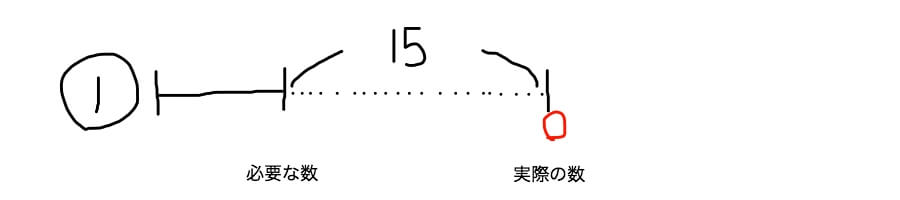



中学受験 差集め算の解き方は3パターン 線分図を書きましょう



2



差集め算 とりちがえ問題を表 面積図 消去算で解いてみよう みみずく戦略室



第2章 差集め算の 偏差値アップ 指導法 例題 中学受験の勉強法 偏差値アップの学習法




算数文章題講座 差集め 過不足算の解き方 基本問題
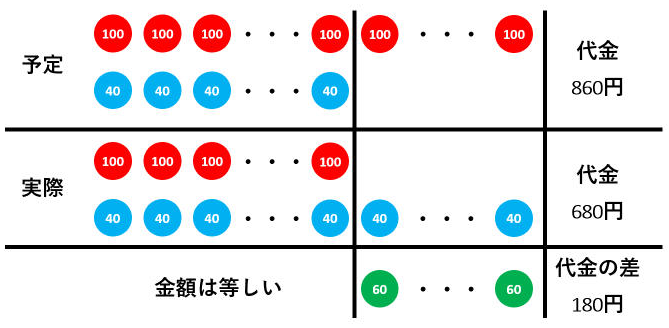



差集め算 とりちがえ問題を表 面積図 消去算で解いてみよう みみずく戦略室
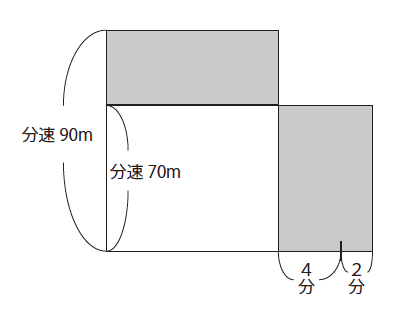



差集算を面積図で解く2 プロ家庭教師 俵屋の日記




中学受験 算数確認チェック12 和と差の文章題 つるかめ 差集め算 グランパは元塾長




中学受験 差集め算とは 基本問題はできるのに応用問題ができない理由 かるび勉強部屋




中学受験 差集め算 過不足算 解き方と考え方 Youtube
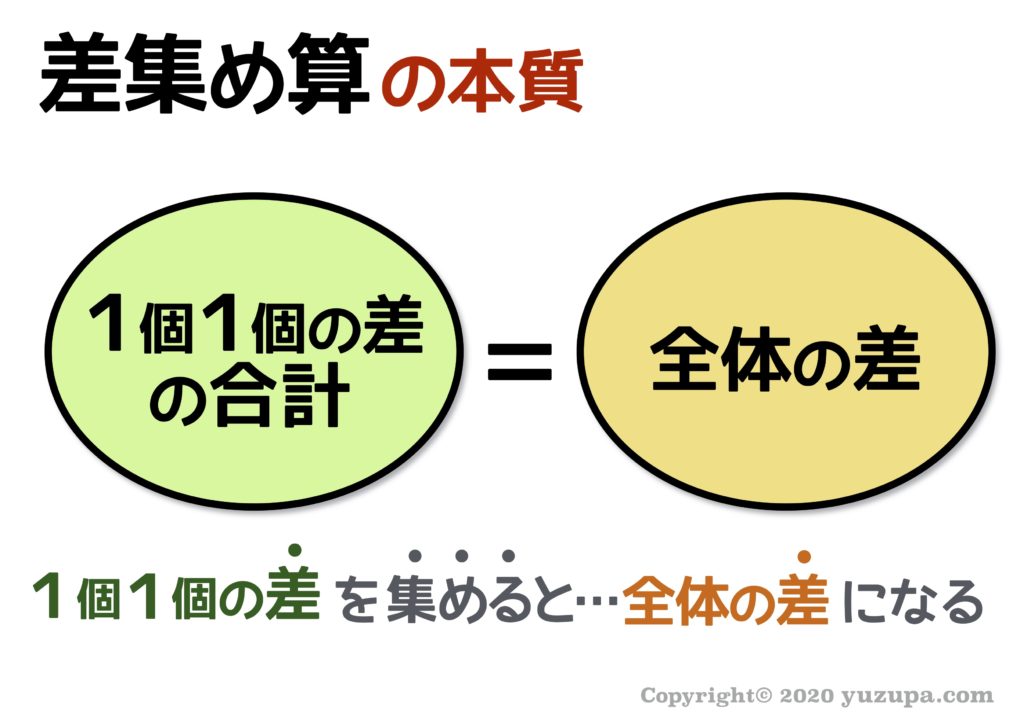



中学受験 差集め算とは 基本問題はできるのに応用問題ができない理由 かるび勉強部屋
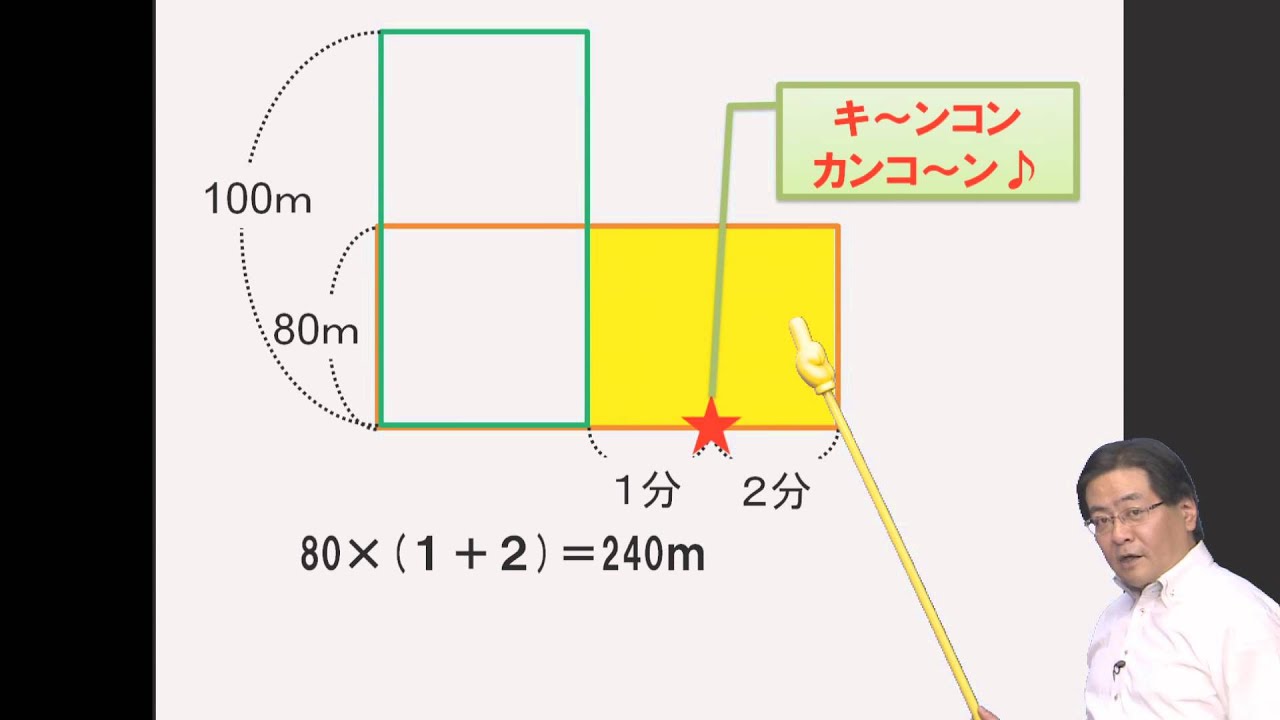



差集め算 Youtube




中学受験 差集め算とは 基本問題はできるのに応用問題ができない理由 かるび勉強部屋




中学受験 差集め算の解き方は3パターン 線分図を書きましょう




差集算 差集め算 線分図と面積図で解こう



過不足算 差集め算 基礎から入試問題まで 父ちゃんが教えたるっ
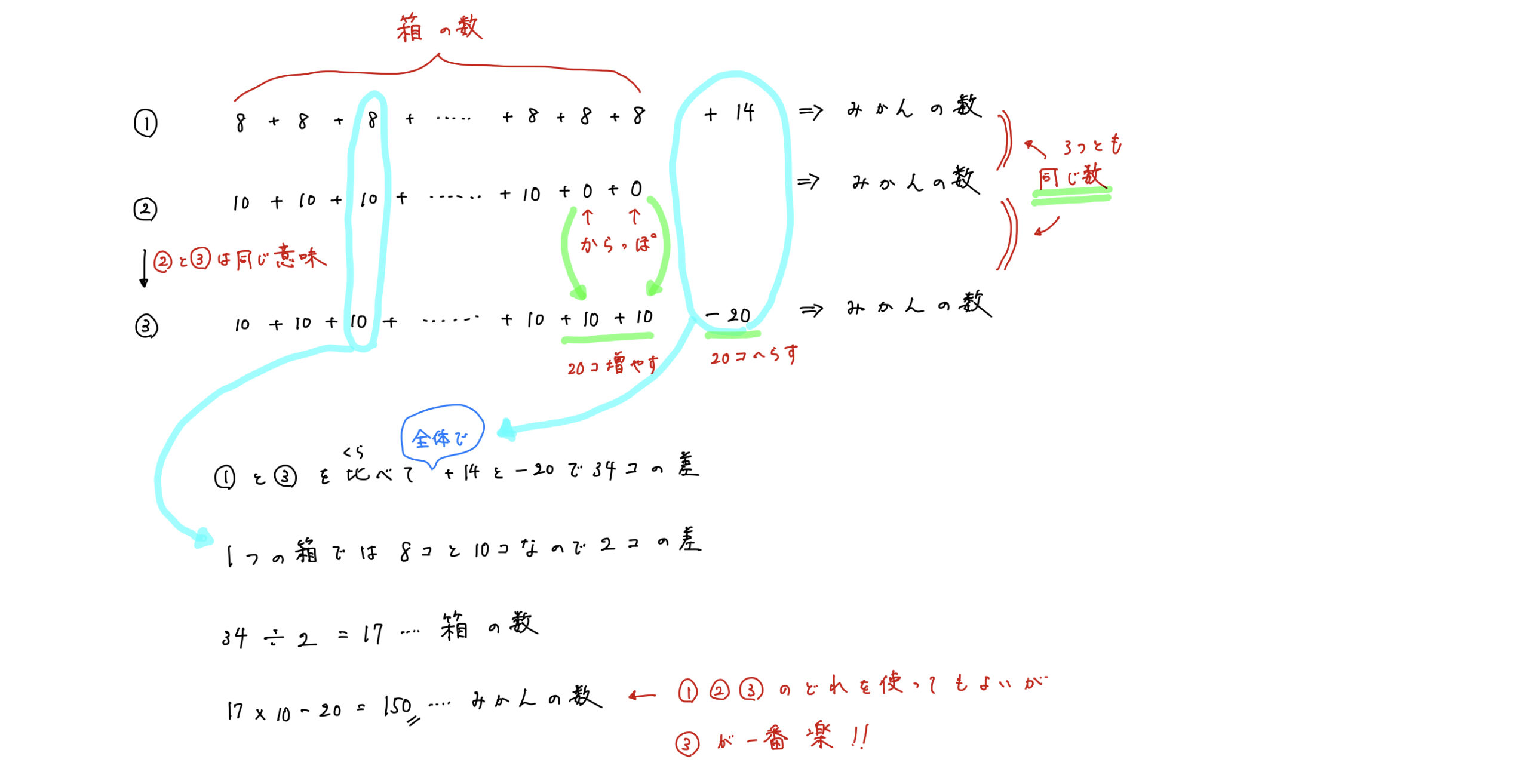



差集め算 長椅子の問題 お菓子を配る問題 和差算 中学受験算数 カテキョウブログ




差集め 過不足算 基本 中学受験準備のための学習ドリル




全体の差 と 1つあたりの差 に注目しよう 過不足算 差集め算の解き方 中学受験ナビ
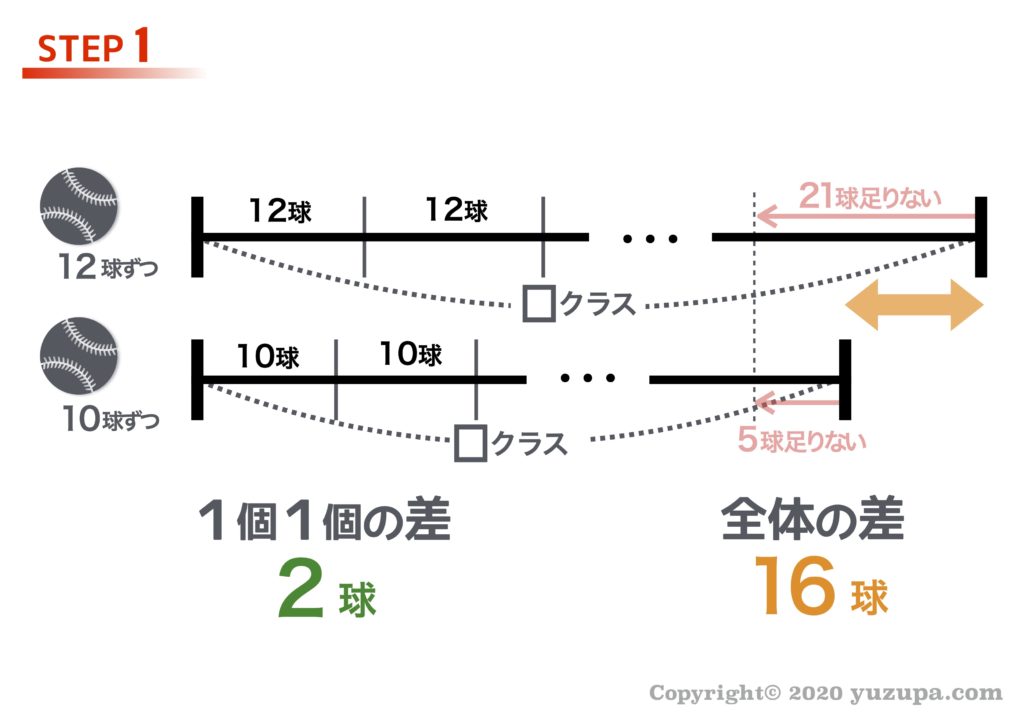



中学受験 差集め算とは 基本問題はできるのに応用問題ができない理由 かるび勉強部屋




4月12日 小5算数 ジャングルジムブログ




7 差集め算 青空塾の教え方




7 差集め算 青空塾の教え方




算数の教え方講座 差集め算 過不足算 応用 10ken Site Osiekata Youtube



2




差集め算が分からない 教え方のコツとは 文章問題編 オンライン家庭教師 スタディメンター



No comments:
Post a Comment